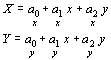
The most common transformation is Affine Polynomial. Affine transformations are a subset of bilinear transformations. Bilinear transformations account for rotation, shift, and differential scaling in X and Y. The X and Y axis orthogonality may change, but parallel lines remain parallel. Affine polynomial transformations of a plane change squares into parallelograms and change circles into ellipses of the same shape and orientation. The affine polynomial transformation results may not be as good as when using a higher order polynomial.
The minimum number of control points required for this transformation is three, though four are required to calculate an RMS value.
The general form for affine transformations is:
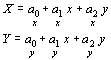
This is called the six parameter affine polynomial transform.

The left graphic is the file before using the affine polynomial transformation. The right
graphic is the file after an affine polynomial transformation. Note that lines remain parallel.